¿Qué es un Histograma?
Un histograma mide el número de pixeles con una determinada intensidad en una imagen.
Por ejemplo, en la siguiente imagen y su histograma:

Los pétalos del girasol tienen intensidades de gris claras cercanas a 255 y la ventana de la esquina superior izquierda tienen intensidades de gris oscuras cercanas a 0.
Entonces existen aproximadamente:
2000 pixeles con intensidad 50,
22000 pixeles con intensidad 100,
1000 pixeles con intensidad 150, y así sucesivamente. (De acuerdo al gráfico de la derecha.)
De acuerdo a su histograma, las imágenes se pueden ser:
- Oscuras: Si la mayoría de sus pixeles se encuentran en la zona izquierda del histograma.
- Claras: Si la mayoría de sus pixeles se encuentran en la zona derecha del histograma.
- Bajo contraste: Si la mayoría de sus pixeles se encuentran en la zona central del histograma.
- Alto contraste: Los pixeles se encuentran distribuidos en todo el ancho del histograma.
Con la ecualización del histograma las imágenes oscuras, claras, y de bajo contraste se transforman en imágenes de alto contraste (generalmente).
Las imágenes de alto contraste están optimizadas respecto a su distribución de intensidades y casi no se logra mejorías notorias con la técnica de ecualización.
Técnica de ecualización con MATLAB
Para ecualizar una imagen oscura, clara o de bajo contraste se siguen los siguientes pasos:
|
L=256; for m=0:L-1 p= (image == m); image_hist(m+1)=sum(sum(p)); end |
El programa es un bucle que recorre todas las intensidades de gris de una imagen de 8 bits. En 'p' se almacena una imagen lógica cuyos valores son: 0 si no existe coincidencia en la comparación y 1 si existe coincidencia. Luego se suman todas las coincidencias del valor del pixel dado en 'm' y se almacena el valor en un vector 'image_hist' que es el histograma de la imagen. Al graficar,
|
n=0:L-1; figure; stem(n,image_hist,'filled','markersize',2) axis([0 L-1 0 max(image_hist+10)]) |
Se obtiene el gráfico a la derecha de la imagen del girasol.
2. Se halla la transformación lineal para obtener la nueva imagen a partir del histograma de la imagen original. Esto se obtiene sumando y normalizando las probabilidades de los pixeles de la imagen original. De acuerdo a la siguiente fórmula:
Ya que las imágenes son digitales, tienen valores discretos de intensidad; por lo tanto la integral de la fórmula anterior se transforma en sumatoria, del siguiente modo:
Donde 'NM' es la cantidad total de pixeles de la imagen y 'n' es el numero de pixeles de cada intensidad en la imagen. Como el limite superior de la sumatoria varia de 0 a L-1, existirán L sumatorias, las cuales son acumulativas. Una sumatoria acumulativa se puede realizar en MATLAB por medio de la función 'cumsum()' del siguiente modo:
| Tr=((L-1)/size(image,1)*size(image,2))*cumsum(image_hist) |
En particular, no soy partidario del uso de funciones predefinidas en MATLAB, por lo que prefiero usar el siguiente algoritmo de suma acumulativa:
|
s=zeros(1,L); st=0; for k=1:L st=st+image_hist(k); s(k)=st; % Paso principal del algoritmo end % Transformacion lineal Tr=((L-1)/(size(image,1)*size(image,2)))*s; Tr=round(Tr); % redondeamos al mas cercano entero |
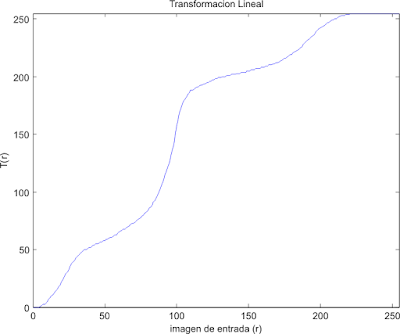
La gráfica de la transformación lineal para la imagen del girasol es:
El girasol se considera una imagen de alto contraste, según su histograma. Para imágenes como el girasol, la transformación lineal resulta similar a una función lineal T(r)=r osea; la imagen de entrada es muy similar a la imagen transformada, no resultando ninguna mejora aparente en la imagen que se desea ecualizar.
3. Como último paso se aplica la transformación lineal a la imagen original. Esto se realiza con el siguiente código:
| image_out=zeros(size(image)); for k=0:L-1 layer = Tr(k+1)*(image==k); image_out = image_out + layer; %suma por capas end |
Finalmente, pongo ejemplos de la transformación lineal para imágenes oscuras, claras y de bajo contraste. En la fila superior se muestra la imagen original y la imagen ecualizada y en la fila inferior se muestra el histograma de la imagen original y la transformación lineal obtenida a partir de su histograma.
Imagen Oscura
Imagen Clara
Imagen de bajo contraste
Fuente consultada: Digital Image Processing, R. Gonzalez, R. Woods, 3ra edición. Pag. 122.



No hay comentarios:
Publicar un comentario